Résumé
- Rayonnement solaire Le
- mouvement du Soleil depuis la Terre
- Le mouvement apparent du Soleil
- Irradiation solaire Obstacles accidentels
- à la lumière du soleil
- en Belgique
- Construction d’un diagramme solaire
A lire également : Quels sont les avantages de la domotique pour votre logement ?
Plan de l'article
Rayonnement solaire
En tant que source d’énergie, la lumière du soleil est un facteur climatique que nous sommes intéressés à exploiter (passivement, à travers des ouvertures vitrées et/ou actif pour produire de l’énergie), mais qui peut également être protégé pour éviter la surchauffe dans été.
Le contrôle de l’énergie solaire nécessite donc de connaître la position correcte du soleil (hauteur et azimut), ainsi que l’intensité du rayonnement à tout moment.
Lire également : Les refroidisseurs adiabatiques : un investissement rentable sur le long terme
L’ énergie renouvelable, inépuisable à l’échelle humaine
Le soleil est un réacteur à fusion nucléaire qui fonctionne depuis cinq milliards d’années. Grâce à un processus de transformation de l’hydrogène en hélium, il émet d’énormes quantités d’énergie dans l’espace (sa puissance est estimée à 63 500 kW/m²). Ce rayonnement s’échappe dans toutes les directions et se déplace dans l’espace à une vitesse constante de 300 000 km par seconde, connue sous le nom de vitesse de la lumière. Après avoir parcouru une distance d’environ 150 millions de kilomètres, l’irradiation solaire atteint l’extérieur de l’atmosphère terrestre avec une puissance d’environ 1 367 W/m². C’est ce qu’on appelle une constante solaire. La Terre, une petite boule comparée au Soleil, intercepte une si petite partie de l’énergie rayonnant du soleil que les rayons du soleil se sont arrêtés semblent constituer un faisceau parallèle.
L’ énergie solaire, l’énergie la plus abondante sur Terre, est la source du cycle de l’eau, du vent et de la photosynthèse, qui est la source des combustibles fossiles. C’est toute la vie sur Terre qui dépend de cette source d’énergie. Heureusement pour l’humanité, selon les astronomes, le soleil ne devrait pas sortir avant 5 milliards d’années.
Une énergie de flux, diffuse et intermittente
Les théories actuelles présentent le rayonnement solaire comme une émission de particules. Ce flux de particules, appelé photons, atteint la terre avec différentes longueurs d’onde auxquelles il correspond à une énergie spécifique décrite par la relation :
E = hv = h. c/λ
Avec,
- λ : longueur d’onde.
- v : fréquence.
- c : vitesse de la lumière.
La distribution de l’énergie des différentes longueurs d’onde du rayonnement électromagnétique du Soleil est appelé le spectre solaire.
****2
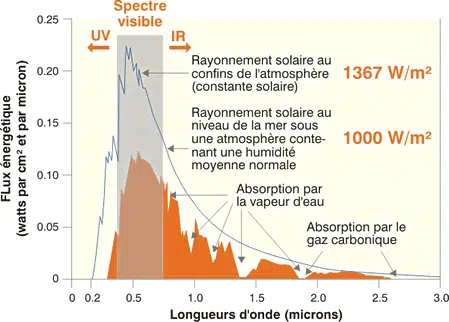
Avec sa température d’émission de 5 500 °C, le soleil rayonne la majeure partie de son énergie à des fréquences élevées (courtes longueurs d’onde). La lumière visible représente 46% de l’énergie totale émise par le soleil. 49% du rayonnement énergétique émis par le soleil est au-delà du rouge visible, dans l’infrarouge. C’est ce rayonnement que nous ressentons comme une onde de chaleur. Le reste du rayonnement solaire, ultraviolet, représente tous les rayonnements de moins de longueur d’onde que celui de l’extrémité violette du spectre visible.
 |
|
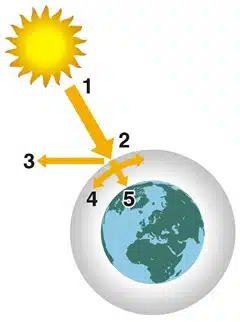
Au moins 35% des rayonnements solaires interceptés par la Terre et son atmosphère se reflètent vers l’espace. Une partie du rayonnement atteignant la Terre a été dispersée dans toutes les directions pendant le passage de l’atmosphère, trouvant des molécules d’air, des aérosols et des particules de poussière (c’est ce rayonnement diffus, appartenant en particulier à la frange bleue du spectre visible qui est responsable de la couleur bleue du ciel clair ). D’autre part, la vapeur d’eau, le dioxyde de carbone et l’ozone de l’atmosphère absorbent 10 à 15% du rayonnement solaire. Le reste du rayonnement frappe directement à la surface.
Outre la composition de l’atmosphère, le facteur le plus important pour évaluer la quantité de rayonnement solaire atteignant la surface de la Terre est l’épaisseur de l’atmosphère à travers laquelle le rayonnement doit passer.
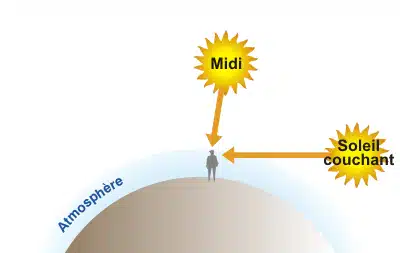
Non Au milieu de la journée, le Soleil est au-dessus de nos têtes, et ses rayons doivent traverser une plus petite épaisseur d’air avant d’atteindre la Terre. Mais au début et à la fin de la journée, le Soleil est bas à l’horizon ; le passage de l’atmosphère est alors plus long. L’atmosphère absorbe et diffuse plus de particules lumineuses parce qu’elle est plus épaisse et plus dense. Ainsi, au coucher du soleil, les rayons sont suffisamment affaiblis pour permettre à l’œil humain de fixer le soleil sans trop d’éblouissement. D’autre part, lorsque l’altitude monte, la couche d’atmosphère à traverser est réduite : dans les régions montagneuses, l’intensité du rayonnement augmente sensiblement.
L’ épaisseur de l’atmosphère traversée influence ainsi le spectre lumineux reçu. Les normes internationales définissent différents types de spectre : AM1 (pour la masse d’air 1, lorsque le rayonnement passe à travers une épaisseur de l’atmosphère), AM0 (spectre sur la surface extérieure de l’atmosphère), AM1.5 (spectre utilisé pour des essais normalisés de panneaux solaires correspondant au passage d’une atmosphère et demie).
Le rayonnement solaire reçu sur une surface varie donc au fil du temps, en fonction de la position du Soleil et de la couverture nuageuse. L’énergie solaire maximale à la surface de la Terre est d’environ 1000 W/m² pour une zone perpendiculaire aux rayons.
****6
L’ énergie solaire à différents cieux.
Le mouvement Terre-Soleil
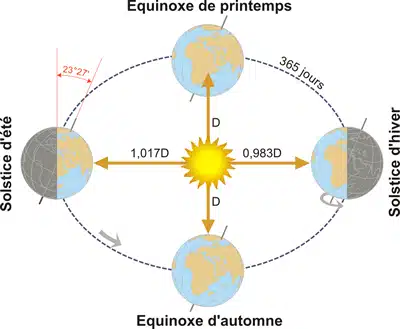
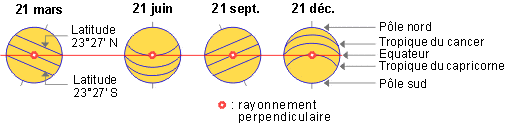
La course terrestre autour du Soleil décrit une ellipse légèrement aplatie. Dans cette ronde annuelle autour du Soleil, la Terre fait un tour complet d’elle-même en 24 heures autour de l’axe des pôles. Cet axe nord-sud a un angle de 23°27′ avec une direction perpendiculaire au plan de l’orbite terrestre autour du Soleil.
Cette pente est constante tout au long de la course autour du Soleil et est responsable de Ainsi, pendant nos mois d’hiver, dans l’hémisphère nord, la durée de l’insolation est relativement courte et le soleil ne se lève pas trop haut dans le ciel, tandis que l’été règne sur l’hémisphère sud. Pendant nos mois d’été, la situation est inversée, l’hémisphère nord fait face au Soleil. Les jours sont plus longs que les nuits dans l’hémisphère nord, et le rayonnement incident approche la verticale.
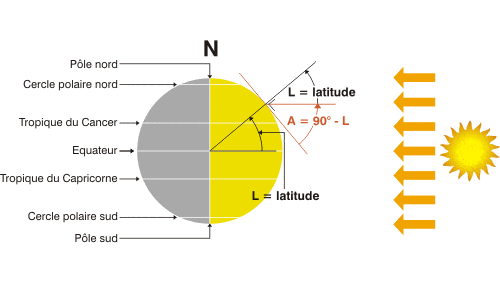
Dans les équinoxes de printemps et d’automne (21 mars, 21 septembre), à midi, le rayonnement est perpendiculaire à l’équateur (latitude 0°) et dans le monde entier, jours et nuits ont la même durée. C’est à ce moment que la hauteur du Soleil à midi est la plus facile à calculer. En fait, sa hauteur est égale à l’angle complémentaire de latitude.
H = 90° — L
****9
Sur le solstice d’été (21 juin), la terre est inclinée vers les rayons du soleil, et à midi ils sont perpendiculaire au tropique du cancer (23°27′ de latitude nord). Le Soleil ne se couche jamais dans les zones du globe dans le cercle arctique (23°27′ au-dessous du pôle Nord). Une personne vivant à la latitude de 66°33′ N. (90°-23°27′) doit surveiller jusqu’à minuit pour voir le Soleil errer dans le nord, descendre pour toucher l’horizon et recommencer à remonter vers le secteur est du ciel. La hauteur du Soleil à midi (solaire) est 23°27′ plus élevée que celle de l’équinoxe.
H = 90° — L 23°27
****10
Sur le solstice d’hiver (22 décembre), l’angle d’inclinaison est inversé et le tropique du Capricorne (23°27′ de latitude S) présente un rayonnement perpendiculaire. La hauteur du soleil à midi est 23°27′ plus basse que celle de l’équinoxe.
H = 90° — L — 23°27′
Le mouvement apparent du Soleil
Comprendre et utiliser pleinement l’influence du Soleil dans le choix et le traitement d’un site, il est clair qu’il faut connaître à tout moment la position du Soleil dans le ciel. Cette information est essentielle pour le calcul des entrées solaires, pour le choix de l’exposition d’un bâtiment, l’installation de systèmes solaires actifs (thermiques ou photovoltaïques), la disposition des parties extérieures adjacentes, l’éclairage naturel des pièces intérieures, l’emplacement des fenêtres, la protection solaire et végétation, etc.
À un certain point, la hauteur et l’azimut du Soleil déterminent la position du Soleil dans le ciel. Ainsi, la direction du rayonnement solaire est connue et peut être calculée Surfaces ensoleillées du bâtiment. Ces calculs prendront en compte les effets de l’ombrage dû au relief, à la structure construite, à la végétation ou au bâtiment lui-même.
****12
En un seul endroit,
- La hauteur «
» du Soleil est l’angle que la direction du Soleil fait par rapport au plan horizontal. Compte de 0° à 90° de horizon vers la voûte céleste.
» du Soleil est l’angle que la direction du Soleil fait par rapport au plan horizontal. Compte de 0° à 90° de horizon vers la voûte céleste. - L’ azimut «
» du Soleil est l’angle créé entre le plan vertical passant par le Soleil et le lieu considéré, et le plan vertical N-S. Cet angle est de 0° vers le sud et est conventionnellement positif à l’ouest et négatif à l’est.
» du Soleil est l’angle créé entre le plan vertical passant par le Soleil et le lieu considéré, et le plan vertical N-S. Cet angle est de 0° vers le sud et est conventionnellement positif à l’ouest et négatif à l’est. 
****15
Pour plus de clarté, le trait solaire est généralement représenté par un diagramme en coordonnées rectangulaires.
****16
Diagramme solaire cylindrique pour Uccle en temps universel.
En savoir plus sur la construction d’un diagramme solaire : LINKS (dernier point).
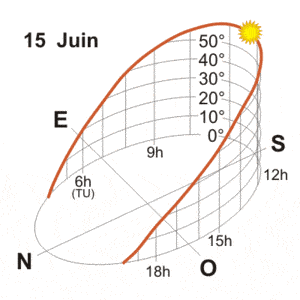
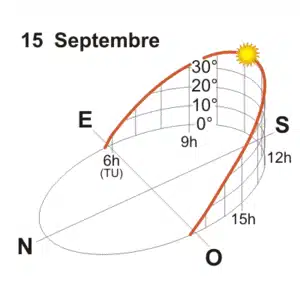
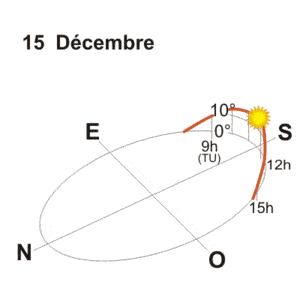
En regardant plus précisément la valeur de l’azimut à différents moments de l’année, nous constatons que l’expression « le soleil se lève à l’est et se couche à l’ouest » n’est pas exacte. En effet, en décembre, elle monte vers le sud-est pour se tenir au sud-ouest, tandis qu’en juin elle s’élève pratiquement à la nord-est pour rester au nord-ouest. Cela donne un maximum de 7 heures de soleil en décembre et plus de 16 heures en juin : ce sont les deux périodes solstices de l’année. Ce n’est qu’aux équinoxes de printemps et d’automne que la durée de la journée est égale à celle de la nuit.
Quant à la hauteur du Soleil, il a atteint un sommet de 62° le 21 juin à 12 fois (temps universel), tandis que le 21 décembre un 12 huniv. Il n’atteint que 16°.
Les graphiques et tableaux suivants donnent à Uccle la hauteur et l’azimut du Soleil, selon le temps universel, pour les mois de mars, juin, septembre et décembre.
****17
| Météo | Dim : degré de hauteur | Dim : degré d’azimut |
|---|---|---|
|
7 8 9 10 11 12 13 14 15 16 17 |
8.7 17.5 25.3 31,6 35,5 36,7 34,7 30,1 23.4 15.2 |
— 75,1 — 62,7 — 48,9 — 33,4 — 16,0 2.5 20,8 37,7 52,8 66,1 78.3 |
| Tempo | Sol : Grau de altura | Sol : Grau de azimute |
|---|---|---|
| 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | 3.1 11.4 20.4 29.9 39,3 48,3 56,0 61,2 62,3 58,7 51,8 43.2 33,9 24.4 15.2 6,5 | — 124,0 — 112,9 — 102,1 — 90,9 — 78,7 — 64,1 — 45,5 — 20,7 8.6 35,8 56,9 72,9 85,9 97,4 108,3 119,2 |
| Tempo | Sol : Grau de altura | Dim : degré d’azimut |
|---|---|---|
| 6 7 8 9 10 11 12 13 14 15 16 | 6.0 15.4 24.3 32,1 38.3 41,9 42,3 39,6 34,0 26.6 17.9 | — 87,9 — 76,0 — 63,2 — 48,7 — 31,9 — 12,9 7.4 26.9 44,3 59,4 72,6 84,7 |
| Météo | Dim : degré de hauteur | Dim : degré d’azimut |
|---|---|---|
| 8 9 10 11 12 13 14 | 1,9 8.3 12.9 15,5 15,8 13.8 9.6 | — 48,3 — 36,1 — 22,9 — 8,9 5.4 19.5 32,9 45,4 |
Incident d’irradiation solaire
L’ angle que les rayons du soleil font à une surface détermine la densité d’énergie reçue par la surface. Une fois que le rayonnement solaire arrive sur Terre un faisceau parallèle, une surface perpendiculaire à ces rayons intercepte la densité d’énergie maximale. Et si nous inclinons la surface de cette position perpendiculaire, son éclairage diminue.
La meilleure façon de représenter ce phénomène est peut-être de découvrir les rayons parallèles du Soleil par une poignée de crayons tenus en main sur une feuille de papier, pointes en bas. Les marques faites par les pics représentent des grains d’énergie. Lorsque les crayons sont perpendiculaires à la feuille, les pointes sont serrées au maximum : la densité d’énergie par unité de surface est la plus grande. Lorsque nous inclinons tous ces crayons parallèles ensemble, les pointes dévient et couvrent des surfaces de plus en plus allongées : la densité d’énergie diminue avec la propagation des traits.
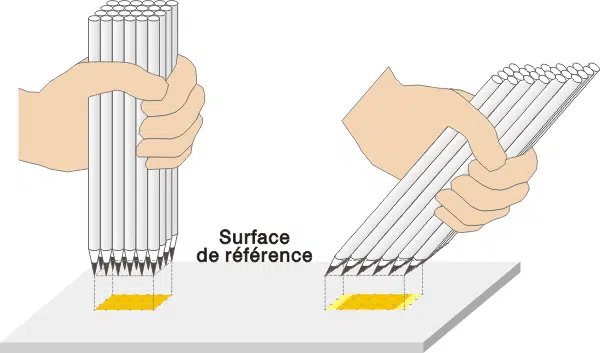
Cependant, une surface qui dévie de 25% de cette position perpendiculaire au Soleil intercepte même plus de 90% du rayonnement direct maximal. L’angle que les rayons du soleil faire avec la surface normale (angle d’incidence) déterminera le pourcentage de lumière directe interceptée par la surface. Le tableau ci-dessous montre les pourcentages de lumière interceptée par une surface pour différents angles d’incidence.
****22
En réalité, le rayonnement total reçu sur une surface, appelé irradiation solaire fortuite (ou éclairage d’énergie globale), est défini par la somme de trois composantes :
- Irradiation directe, venant directement du soleil. Ce composant est annulé si le Soleil est masqué par des nuages ou par un obstacle.
- Irradiation diffuse, correspondant au rayonnement reçu de la voûte céleste, à l’exclusion du rayonnement direct. Cette énergie diffusée par l’atmosphère et dirigée vers la surface de la Terre, peut atteindre 50% du rayonnement global reçu, lorsque le Soleil est bas à l’horizon, et 100% vers un ciel entièrement nuageux.
- Irradiation réfléchi, correspondant au rayonnement réfléchi par l’environnement extérieur, en particulier le sol, dont le coefficient de réflexion est appelé « albédo ».
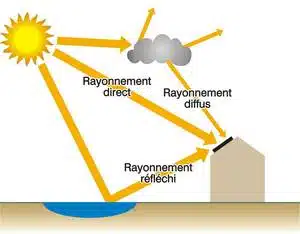
En particulier, l’irradiation hémisphérique est également définie comme l’irradiation générale reçue sur une surface horizontale (la composante réfléchie du sol est nulle dans ce cas). L’éclairage global de la puissance est mesuré par un solarimètre en fonction de la pente et de l’orientation souhaitées. L’éclairage de puissance diffuse par lui-même est mesuré par un solarimètre de bande d’ombre : c’est le même instrument équipé d’un ruban semi-circulaire qui, ajusté périodiquement, masque la lumière directe du soleil de l’appareil de mesure.
La quantité d’énergie reçue dépendra de cette puissance, mais aussi de la durée de la lumière du soleil.
****24
Irradiation solaire annuelle et ressources énergétiques connues par rapport à la consommation annuelle de l’énergie mondiale.
Et cette énergie reçue est énorme ! Même si toute l’énergie solaire reçue sur Terre n’est pas exploitable, on estime que la part qui pourrait être reçue est trois fois supérieure à l’énergie consommée à l’échelle mondiale. Cette énergie, qui semble inépuisable à l’échelle humaine, est totalement respectueuse de l’environnement : son utilisation ne produit pas de déchets ni d’émissions polluantes. Un vrai défi pour l’avenir !
Barrières au soleil
| Les masques solaires peuvent être causés par le relief, la végétation existante, les bâtiments voisins ou par des dispositifs architecturaux attachés au bâtiment lui-même. |
Les bâtiments sont des écrans fixes pour votre quartier. Son rôle peut être positif si nous recherchons une protection contre le soleil : c’est le cas dans les villes méditerranéennes traditionnelles, où les ruelles étroites et la hauteur des bâtiments réduisent rayonnement significativement direct et fournir une ombre bienvenue.
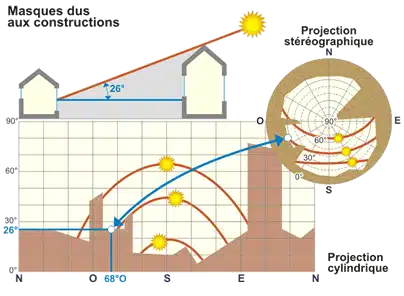
D’un autre côté, ce rôle peut être négatif si les bâtiments voisins cachent le soleil tandis que l’on veut bénéficier de contributions solaires. En fait, dans notre climat, pendant les mois d’hiver, environ 90% des apports solaires se produisent entre 9h et 15h solaire. Tous les masques environnementaux (grands bâtiments ou arbres, qui interceptent le Soleil pendant ces heures) entraveront grandement l’utilisation des gains solaires.
Dans le cas d’un projet solaire passif, il sera donc important de mesurer l’impact de cet effet de masquage. Pour ce faire, les courbes de la course solaire annuelle et la silhouette des bâtiments voisins seront représentées sur un diagramme cylindrique ou stéréographique (figure ci-dessus). Cela permettra d’identifier facilement les périodes où la lumière solaire est disponible et les facteurs de réduction des gains solaires peuvent être calculés.
L’ utilisation de matériaux réfléchissants (verre) peut également influencer l’exposition réelle d’un bâtiment. Ainsi, un bâtiment orienté vers le nord et avec un grand vitrage clair pour profiter de la lumière naturelle peut être trouvé dans une position sud si un bâtiment est construit en face avec un vitrage réfléchissant, précisément pour se protéger de la lumière du soleil. De toute évidence, les conditions de confort dans le premier bâtiment sont profondément modifiées par la construction du second bâtiment.
Soleil en Belgique
Sous notre climat, le Soleil nous apporte chaque année environ 1.000 kWh/m² dans le sol, l’équivalent énergétique de 100 litres de fioul par m² !
****
La quantité d’énergie solaire reçue en un seul endroit est répartie inégalement au fil des saisons. Il varie en fonction du jour et de l’heure considérés et est influencé par les conditions météorologiques et par les niveaux de pollution atmosphérique. Il est généralement considéré que 250 kWh sont reçus du 15 octobre au 15 avril et 750 kWh du 15 avril au 15 octobre.
****29***** 30
Selon les conditions climatiques, le rayonnement nous atteindra en fonction de ses composants diffus et directs dans une proportion plus ou moins grande.
****31
N.B. : Le rayonnement solaire global est considéré ici sur une surface horizontale (sur laquelle la composante réfléchie du rayonnement est nulle).
Dans la pratique, les conditions climatiques peuvent être caractérisées par une insolation directe relative : c’est la relation entre l’insolation effective (S) et l’insolation maximale théorique (So). Cela détermine les types de ciel :
- Un ciel est considéré comme serein lorsque l’insolation directe relative est comprise entre 80 et 100%,
- un ciel est considéré comme moyen lorsque l’insolation directe relative S/So est entre 20 et 80 %,
- un ciel est considéré comme nuageux lorsque le coup de soleil direct relatif S/So est compris entre 0 et 20%.
| Ciel | Mois de l’année | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| J | F | M | A | M | J | J | A | S | À propos | N | D | |
| Couvert | 65 | 54 | 45 | 40 | 30 | 28 | 32 | 29 | 29 | 43 | 61 | 70 |
| Moyen | 23 | 33 | 39 | 44 | 47 | 53 | 52 | 55 | 47 | 37 | 28 | 20 |
| 12 | 13 | 16 | 16 | 13 | 19 | 16 | 16 | 24 | 20 | ! | ! 11 ! |
Et le tableau suivant donne pour Uccle, les moyennes journalières mensuelles de l’insolation directe relativo.
Par exemple, uma insolação direta relative de 34% en mars à Uccle indique qu’en moyenne seulement 34% du temps est ensoleillé entre le lever et le coucher du soleil.
****32
Énergie quotidienne moyenne reçue sur une surface horizontale.
Chaque année, il est d’environ 60% de l’énergie solaire qui nous atteindra sous forme de rayonnement diffus, et 40% sous forme de rayonnement direct.
| Mondial | Direct | Diffus | |
|---|---|---|---|
| Normal | 980 | 40 | 60 |
| 2002 | 990 | 44 | 56 |
| 2003 | 1 151 | 52 | 48 |
| 2004 | 1.034 | 44 | 56 |
| 2005 | 1 056 | 47 | 53 |
| 2006 | 1.040 | 47 | 53 |
| 2007 | 998 | 45 | 55 |
Rayonnement reçu annuel sur une surface de 1m² au soleil. Source de résonance magnétique.
> En Belgique, en raison de la présence fréquente de nuages, plus de la moitié de l’énergie solaire provient de nous de façon diffusée !
Éclairage électrique disponible
Les tableaux suivants fournissent un éclairage solaire direct et mondial pour un ciel serein à Uccle les 15 mars, juin, septembre et décembre.
****33
****34
****35
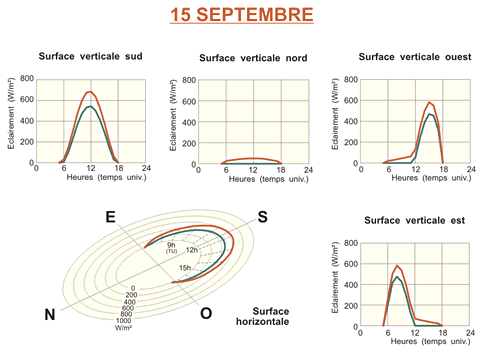
Par exemple, l’éclairage direct et mondial de l’énergie solaire pour un ciel serein à Uccle sont,
- le 15 mars, à 10huniv. (11hoff) 291 W/m² et 424 W/m² pour une surface horizontale,
- le 15 juin à 13huniv. (15hoff) de 124 W/m² et 323 W/m² pour une zone verticale ouest,
- 15 septembre à 13huniv. (15hoff) de 467 W/m² et 687 W/m² pour une surface verticale sud.
Dans les cas où la surface réceptrice est verticale, l’éclairage énergétique sera maximal sur une surface sud en hiver, tandis qu’il sera maximal sur une surface est ou ouest en été. Cependant, la surface verticale n’est jamais la surface la plus favorable pour capturer l’énergie solaire.
Afin de tenir compte des conditions météorologiques, les tableaux ci-dessous montrent l’éclairage global de l’énergie solaire pour le ciel moyen et nuageux, à Uccle (Bruxelles), les 15 mars, juin, septembre et décembre, avec une surface horizontale et une surface verticale orientée sud, nord, est et ouest.
Par exemple, l’éclairage mondial de l’énergie solaire à un ciel moyen et nuageux à Uccle est,
- le 15 mars à 9huniv. (10hoff) 197 W/m² et 89 W/m² pour une surface horizontale,
- 15 Juin à 9huniv. (11hoff) de 419 W/m² et 130 W/m² pour une surface verticale est.
****37
Ciel moyen.
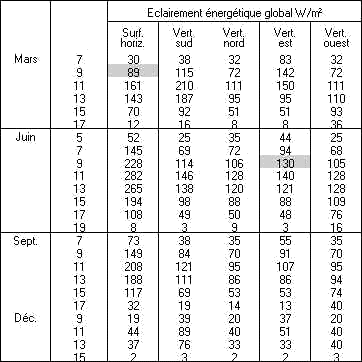
Ciel nuageux.
Par rapport au ciel serein, la réduction de l’éclairage énergétique global sur une surface horizontale est d’environ 30% par ciel moyen et de 70% pour le ciel nuageux. Cette différence est marquée lorsque la surface réceptrice tend à être perpendiculaire au rayonnement solaire.
Variation géographique de l’exposition à l’énergie
Le tableau ci-dessous montre les expositions moyennes mensuelles et annuelles à l’énergie en Wh/m² pour les stations sélectionnées.
| Wh/m2 | MIDDELKERKE | UCCLE | CHIEVRES | FLORENNES | Spa | SAINT-HUBERT | |
|---|---|---|---|---|---|---|---|
| Janvier | 23,324,1 | 19 934,9 | 18.946 | 21,429,49 | 20 193.282 | 21.701,74 | 22 207,33 |
| Février | 38,408,6 | 35 366,7 | 34.13,7 | 37 347,43 | 36 886,284 | 39 867,08 | 42.403 39 |
| Marte | 82 762,2 | 70 736,2 | 70 311,2 | 73 494,77 | 74 980 998 | 75 783,84 | 77 881,23 |
| Avril | 120 012 | 106 964 | 104 289 | 110 814,4 | 108 247,55 | 111 258,9 | 112.953,5 |
| Mai | 155 199 | 142 253 | 133 433 | 142 964,2 | 139 408,37 | 144 247,7 | 147 089,5 |
| Juin | 161 996 | 148 892 | 139.511 | 149 189,7 | 149 189,71 | 152 095,5 | 154 251,2 |
| Juillet | 156.251 | 140.136 | 131 869 | 141 958,6 | 144 339,32 | 144 247,7 | 148 684,1 |
| Aout | 133 588 | 120 135 | 113.045 | 122 898,7 | 120 976,34 | 127 024,1 | 124.579.4 |
| Set. | 97.249,4 | 89 548,8 | 85 518 | 89 726,62 | 90.176.658 | 93 757,5 | 95.727,1 |
| Outubro | 60,666 | 54 359,9 | 54.087.7 | 57 785,18 | 58 599 132 | 61 316,02 | 59 199,18 |
| À propos de Nov. | 288 288,4 | 24 577 | 24.771.4 | 2 132,73 | 26 249 322 | 27 085,5 | 25,560 38 |
| Déc. | 18 576,5 | 15,690,1 | 15 940,2 | 18 120,89 | 16 820,78 | 17 654 ,19 | 18 279,24 |
| ANNEE | 1 076 322 | 968 591 | 925.849 | 9992 862,8 | 986,067,77 | 1 016 040 | 1 028 816 |
La Belgique se caractérise par des variations géographiques relativement faibles, inférieures à ± 5% pour l’ensemble du pays, à l’exception de la région côtière et du pays Gaumáis, avec un écart annuel de 10% par rapport à Uccle et même dépassé ( 18% au Luxembourg).
D’après le tableau précédent, les écarts d’Uccle sont les suivants selon la saison : hiver (H) ; printemps (P) ; été (E) ; automne (A) et période de végétation (V) couvrant mai, juin et juillet.
| H | P | E | UM | V | ||
|---|---|---|---|---|---|---|
| Middelkerke | 13% | 12% | 10% | 10% | 9% | 11% |
| Chièvres | — 3% | — 4% | — 6% | — 2% | — 6% | — 4% |
| Kleine-Brogel | 9% | 2% | 1% | 3% | 1% | 2% |
| Florennes | 4% | 1% | 1% | 4% | 0% | 2% |
| Spa | 12% | 4% | 3% | 8% | 2% | 5% |
| Saint Hubert | 17% | 6% | 4% | 7% | 4% | 6% |
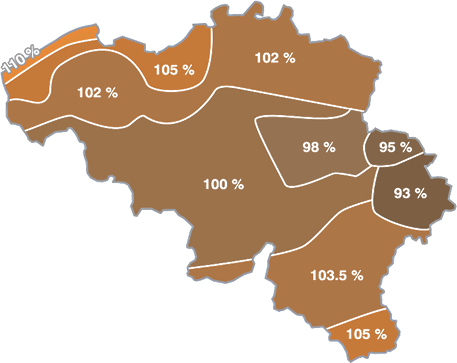
L’ Institut Royal de Météoorologie de Belgique a établi une distribution du rayonnement solaire basée sur la distribution de l’insolation effective selon les zones climatiques de la Belgique, sachant que les variations de ce rayonnement par rapport à Uccle sont approximativement les suivantes :
| Côte | 10% |
| Polders et Waes | de 5% à 2% en fonction de la distance de la zone côtière. |
| Kempine et Flandre | 2% |
| Hesbaye | — 2% |
| Terre de Herve | — 5% |
| Gileppe — Warche | — 7% |
| Plateau Ardennes | 2 % à 5% |
| Pays Gaumáis | 5% |
| Grand-Duché de Luxembourg | 10% |
La carte ci-dessous a été déduite de lui.
L’ influence de l’orientation et de l’inclinaison
Il est clair, bien sûr, que la quantité d’énergie reçue sur une surface dépendra de son orientation et de son inclinaison.
Le graphique ci-dessous montre cette influence dans notre pays (l’azimut se lit sur la circonférence et la hauteur du Soleil dans les cercles intérieurs) :
****40
Une surface inclinée à 38° vers le sud recevra une énergie solaire maximale. Une surface verticale à l’est recevra seulement 50% de cette énergie maximale.
Construction d’un diagramme solaire
La voûte céleste est la partie visible du ciel dans toutes les directions au-dessus de l’horizon. La grille du diagramme solaire représente les angles horizontaux et verticaux des points de la voûte céleste. Tout se passe comme si l’observateur avait vu l’azimut et la hauteur du Soleil dans un hémisphère transparent au-dessus de lui et comme si alors étiré cette partie de la sphère dans un cylindre vertical.
**41**42
Lorsque nous connaissons l’azimut et la hauteur solaire, nous n’avons aucun problème à positionner la position du soleil dans le ciel.
****43
En rejoignant les différents endroits, du Soleil à divers moments de la journée, nous obtenons le chemin de la course du Soleil.
****44
Ainsi, il est possible de suivre la course au soleil pour n’importe quel jour de l’année. Les trajectoires indiquées dans les cartes solaires correspondent au vingtième jour de chaque mois (certains diagrammes donnent pour les 5, 15 et/ou 25 jours de chaque mois). La journée solaire est la plus longue dans le solstice d’été, lorsque le Soleil atteint sa plus haute hauteur et balaie la zone azimutale plus large des deux côtés du sud. A proximité du solstice d’hiver, au contraire, le Soleil est beaucoup plus petit dans le ciel : il reste visible plus longtemps et balaie le secteur azimutal le plus faible.
****45
Enfin, si nous connectons les points correspondant aux mêmes heures dans les différentes courbes par rapport à la même latitude (et à différents moments de l’Enna, nous obtenons pour chaque heure de la journée un une certaine ligne pointillée.
De même, nous pouvons facilement représenter les masques solaires. Il suffira de détecter l’azimut et la hauteur de chacun des obstacles et de les reporter sur le diagramme.